
To reflect objects over horizontal or vertical lines that are not the x- or y-axes, the following steps can be used: Reflection over a horizontal or vertical line All of the points on triangle ABC undergo the same change to form DEF. Triangle ABC is reflected across the line y = x to form triangle DEF. Reflection over y = xĪ reflection across the line y = x switches the x and y-coordinates of all the points in a figure such that (x, y) becomes (y, x). Triangle DEF is formed by reflecting ABC across the y-axis and has vertices D (4, -6), E (6, -2) and F (2, -4). Algebraically, the ordered pair (x, y) becomes (-x, y). In a reflection about the y-axis, the y-coordinates stay the same while the x-coordinates take on their opposite sign. Triangle DEF is formed by reflecting ABC across the x-axis and has vertices D (-6, -2), E (-4, -6) and F (-2, -4). Algebraically, the ordered pair (x, y) becomes (x, -y). In a reflection about the x-axis, the x-coordinates stay the same while the y-coordinates take on their opposite signs. The most common cases use the x-axis, y-axis, and the line y = x as the line of reflection.

There are a number of different types of reflections in the coordinate plane. This is true for any corresponding points on the two triangles and this same concept applies to all 2D shapes. A, B, and C are the same distance from the line of reflection as their corresponding points, D, E, and F. The figure below shows the reflection of triangle ABC across the line of reflection (vertical line shown in blue) to form triangle DEF. The same is true for a 3D object across a plane of refection. In a reflection of a 2D object, each point on the preimage moves the same distance across the line of reflection to form a mirror image of itself. The term "preimage" is used to describe a geometric figure before it has been transformed "image" is used to describe it after it has been transformed. When an object is reflected across a line (or plane) of reflection, the size and shape of the object does not change, only its configuration the objects are therefore congruent before and after the transformation. In geometry, a reflection is a rigid transformation in which an object is mirrored across a line or plane. Notice the lines of reflection intersect at the figure's center below.Home / geometry / transformation / reflection ReflectionĪ reflection is a type of geometric transformation in which a shape is flipped over a line. Multiple lines of reflectionĪ geometric figure can have more than one line of reflection. Point A on the hexagon reflects to A' which is not on the hexagon.Ī line of symmetry is known as a rigid motion (or transformation) in geometry since the figure that is reflected across it does not change size or shape and is only "flipped" across the line of symmetry. Although the line through the vertices of the irregular hexagon below divides it into two equal parts, it is not a line of symmetry.

Not all lines of reflection are also lines of symmetry just because they divide the figure into two equal parts. This is true for any point on the ellipse.
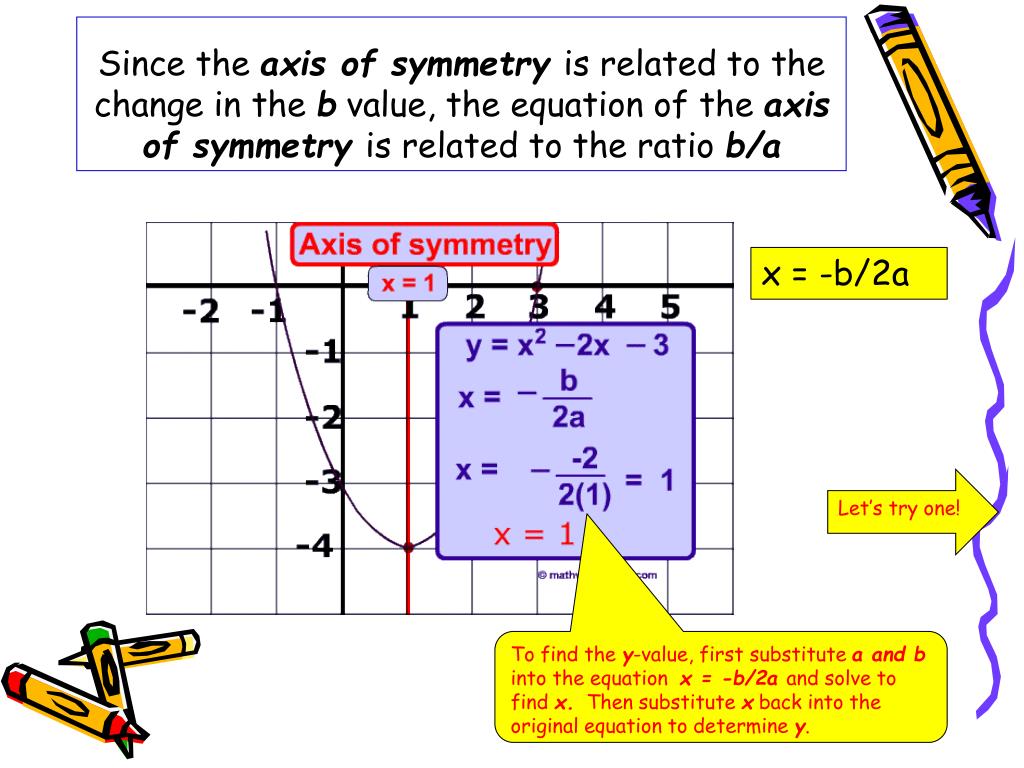
When A and B are reflected across it, they are mapped to A' and B', also on the ellipse. The line that cuts through the major axis of the ellipse above is a line of symmetry. Mathematically, a line of symmetry is a line of reflection that maps any point on the figure back to the figure. In the figure below, the lines of symmetry divide the figures into mirror images. Home / geometry / line / line of symmetry Line of symmetryĪ line of symmetry is a line that divides a figure into two mirror parts.


 0 kommentar(er)
0 kommentar(er)
